理数系学問を勉強・研究されている学生の方は金融業界に馴染みがないかもしれませんが、皆さんの数理的センスや論理的思考力はこの業界で活躍する上で大きな武器となります。腕試しに以下の問題に挑戦してみませんか?
問題1
端に火をつけると7分および10分で燃え尽きる均質な紐がそれぞれ1本ずつある。この2本を使って1分を計測することができるか。
-
解答
7分の紐の片端と10分の紐の両端に同時に火をつけ、10分の紐が燃え尽きると同時に7分の紐のもう片端に火をつけ、計測スタートする。7分の紐が燃え尽きたときに計測を終えるとちょうど1分が計測できる。
10分の紐が燃え尽きた時点で最初に火をつけたときから10分の半分すなわち5 分経過しており、7分の紐が残り2分となっているので、そこから両端を燃やすと2分の半分すなわち1分が計測できる。
問題2
7が80個並んだ80桁の数をXとおく。ここで以下の2種類の操作を考える:
A) 最後の1桁、すなわち一の位を切り離して2 つの数に分け、それらを足す。
例:123 → 12 + 3 = 15
B) 1を足す。
例:123 → 123 + 1 = 124
数Xから始めて、この2種類の操作を無作為に組み合わせて合計88回行ったところで初めて1桁の数になった。この1 桁の数は何か。
例えばXに対してA, A, B, Aと操作すると以下のようになる:
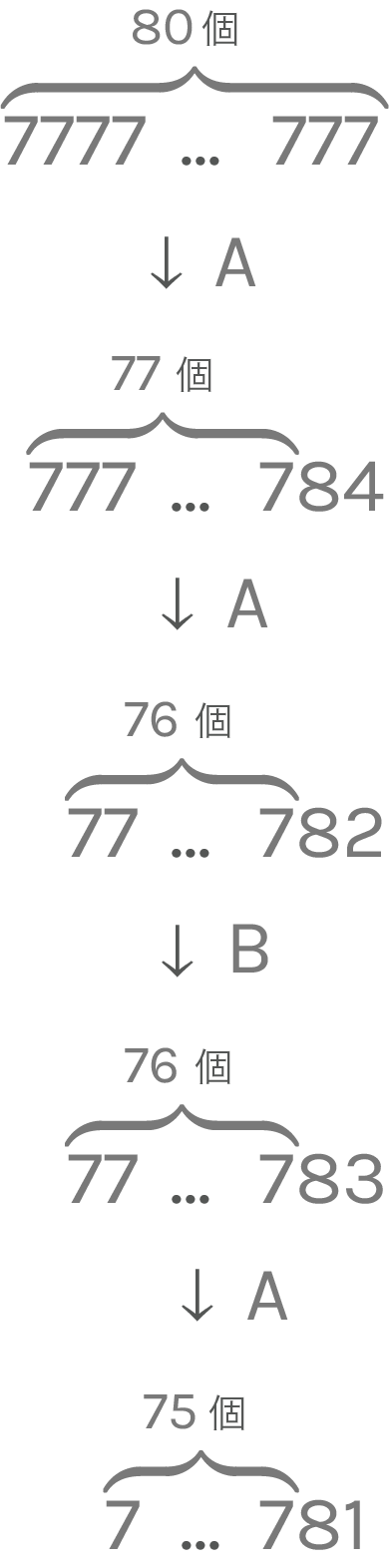
-
ヒント
操作Aによって9で割った余りは保たれます。
-
解答
こちらの問題は、ヒントを参考に是非ご自身で挑戦してみてください!
問題3
1から50までの数が書かれたカードがそれぞれ1 枚ずつ計50枚あり、これを用いた次のゲームを考える。
50枚の中からランダムに1枚を引き、出た数の金額(円)をもらってゲームを終了するか、もらわずにカードを戻してもう一度50枚からランダムに引くかを選ぶ。
2回目に引いた数が1回目の数より大きければ、2回目の数の金額をもらってゲームを終了するか、もらわずにカードを戻してもう一度50枚からランダムに引くかを選ぶ。
2回目の数が1回目の数以下ならば、カードを戻してもう一度50枚からランダムに引く。
3回目の数が2回目の数より大きければ、3回目の数の金額をもらってゲームは終了となり、3回目の数が2回目の数以下ならば、賞金は0円でゲームは終了となる。
このゲームの参加費がいくらならあなたは参加するか。
-
解答
2回目に引いた数がxであるとする。このとき続行して3回目に引いた場合の賞金の期待値をEとすると
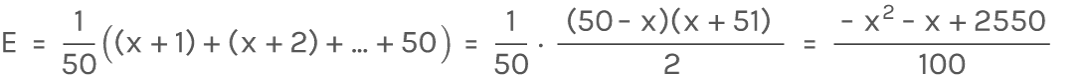
なので、E > x ⇔ x² + 101x − 2550 < 0 ⇔ x ≦ 20 となる。
したがって、- 1回目の数が20以下で続行したとき、2回目が20以下ならば続行、21以上ならば終了を選択することになる。
- 1回目の数がy ≧ 21 で続行したとき、2回目がy以下ならば続行、y + 1 以上ならば終了を選択することになる。
1回目の数が20以下か否かで場合分けする。
- 1回目の数が20以下のとき、続行した場合の賞金の期待値は
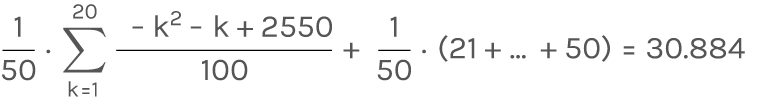
となる。よって1回目が20以下のときは続行を選択することになる。 - 1回目の数がy ≧ 21 のとき、続行した場合の賞金の期待値をE′とすると
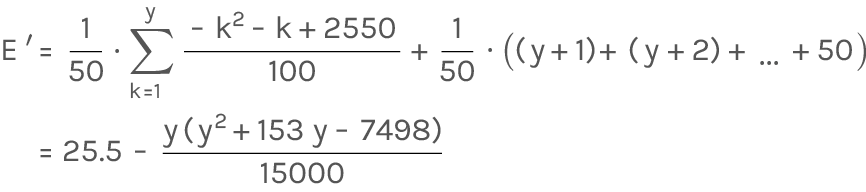
である。
これよりy ≦ 29 ならばE′ > y となり、y ≧ 30 ならばE′ < yとなる。
したがって1回目の数が21以上29以下なら続行、30以上なら終了を選択することになる。
以上より、このゲームの賞金の期待値は

となる。つまり参加費が34円以下なら参加するべきである。 -
コメント
これは「バミューダン・オプション」と呼ばれる金融商品を模して作ったゲームです。これ自体は一つの数学の問題にすぎませんが、実際に取引されている金融商品に似たようなものがあるのです。市場での価格計算はさらに複雑なので、手計算ではなくモデルを使ったコンピュータでの計算となりますが、このような数学的思考はとても役に立ちます。またこのゲームでは50枚のカードが等確率で出ることを仮定していますが、金融の世界では価格が完全にランダムに動くということはなく、市場参加者それぞれの思惑によって価格の「ゆがみ」が生じます。基本的な数学能力に加えて、市場に対する多角的かつ精緻な分析力、様々なピースを組み合わせて論理的に結論を導く思考力を武器に、複雑な金融の世界で収益を上げるのが我々トレーダーの仕事です。
この問題にわくわくした方や挑戦してみたいなと思った方。もしかしたら金融業界であなたの能力を生かせるポジションがみつかるかもしれません。
是非モルガン・スタンレーにご応募ください。
